はじめに

今回ご紹介するZ曲線は、Z字状に分割した空間に順序をつけていく方法で、モートンオーダーはZ曲線を入れ子状に行なった場合の順序の振り方のことです。これらは、空間内の対象の検索や、衝突判定を効率的に行う為の手法の一つです。

Unityなどでアクションゲームを作成している方の中には、なんとなくコリジョンによる衝突判定やバウンスによるIN/OUTの判定をおこなっている方もいらっしゃると思いますが、これらの背景にある（空間充填方法は他にもあるのでこれだけという訳ではない）内容となります。また、GISベースの空間処理、ARでリアルタイムの測距・空間処理をおこなう際に、私が実際に使っているものです。

今回は、Z曲線での空間充填とモートンオーダーについてまとめてみましたので、是非最後までご覧ください。

【Z曲線とインデックス番号】

インデックスの振り方

2次元の場合平面を4分割し、下のようにZになる順序を振ります。

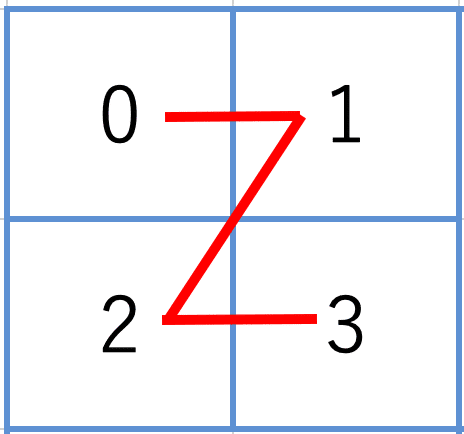
3次元の場合は、こんな感じになります。

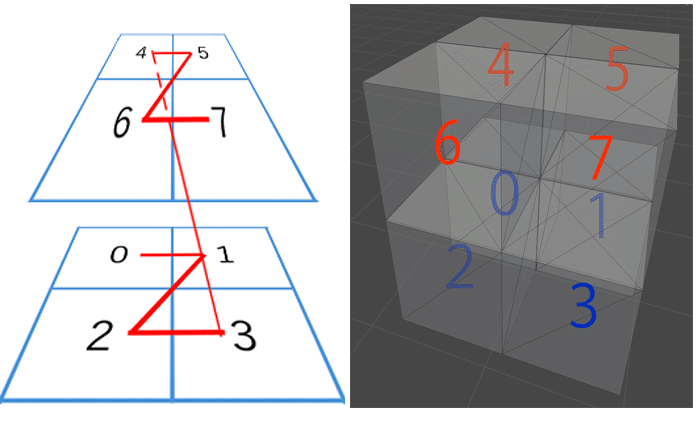
インデックスを2進値にすると、こんな感じになります。

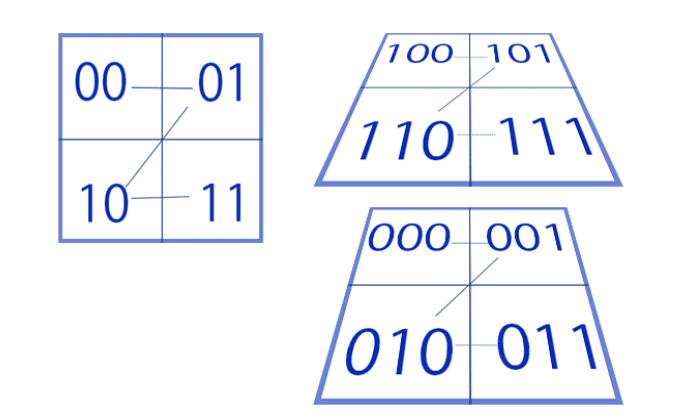
2進のビットに規則性があるのがわかります。

 次に、それぞれのセルを入れ子で4分割してみます。

親側のビットを利用して、インデックス番号を振り直します。

全体で一意になりつつ、Zの構造を維持したインデックスが出来ています。

ネストする毎に（親ビット 子ビット 孫ビット ひ孫ビット…）とすることで、
空間を細分化していきます。

3次元の場合も基本的に同じで、3bit単位で（親ビット 子ビット 孫ビット…）となるだけです。

作り方から逆に考えれば、これは分木ツリーになっており、インデックスコードさえ分かれば、ビットシフトするだけで親空間位置が分かる構造になっているということです。

【空間座標からのインデックス】

空間のインデックスとして数値を割り振りましたが、実際使用する際には空間座標からこのインデックスが分からないと使えません。
数字が各座標とも順列ではないので、単純に幅を割り算で…というわけにはいきませんが、それを少し操作するとインデックスを求めることが出来ます。

分割する空間の辺をLとする。（次軸別々でも問題ありませんが、簡略化のため同じとします。）
分割されたセルの辺は、ネスト数 Nによって 2^N、セルのサイズ L/2^N となります。

1： 座標 (X,Y) /L/2^N とすれば、座標空間からセルが何行何列に相当するかが分かります。

　例として L = 8m、N=3, (X,Y) = (2.5m,5.5m) とすると、セル = (2,5) となり、表からは38番の位置を指しています。

2：行列番号を、それぞれ2進にします。 
　  行が (y1 y2 y3)、列が (x1 x2 x3) とすると、これを (y1x1 y2x2 y3x3) の形で並べます。
　
　上例では (2,5) から 010,101
　並べ替えると、100110

3：これを10進に直すと、表上のインデックスになります。

    上例では、100110 = 38

なんか不思議に見えますが、最初の4分割でビットそれぞれが x,y,z の位置関係に対応していることを思い出していただくと、ああ…なるほど！となると思います。

【大きさのある配置オブジェクトの扱い】

空間を分割してインデックスを振りましたが、空間内にオブジェクトを配置した場合、ネストレベルに応じて下記の赤と緑の枠の様に、バウンスで複数のセルにまたがる状態が考えられます。

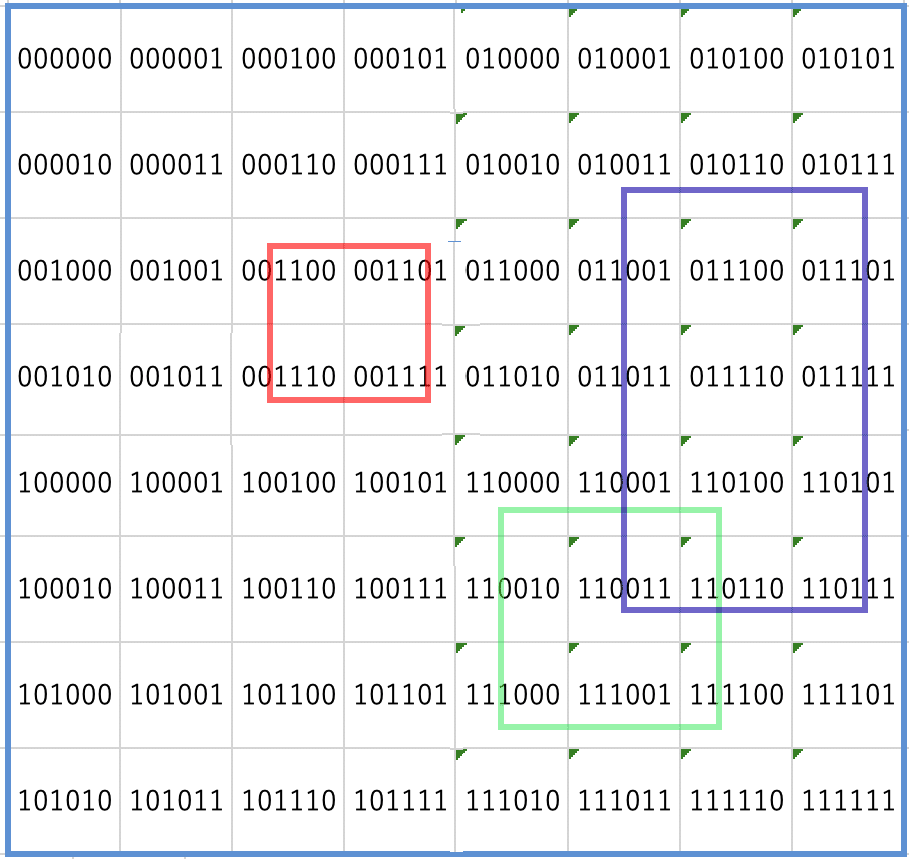
バウンスの左上、右下のインデックス番号を取ると
　　赤　001100,  001111
       緑　110000,  111100
       青    010011,  110111
となっています。

ビットの振り方を思い出してください。

2点のインデックス番号をXORで演算してみます。

4分割を見ると
00 xor 00 = 00, 01 xor 01 = 00, 10 xor 10 = 00, 11 xor 11 = 00
00 xor 01 = 01, 00 xor 10 = 10, 00 xor 11 = 11, 01 xor 11 = 01, 10 xor 11 = 10
区画を跨ぐと、01, 11 いずれかでビットが立ち、同じ区画内だと 00 になることがわかると思います。
階層の上位桁が、上の階層の位置になっているので、上の層から順番に00ではないビットが出たところを探すと、ここが層を跨いでいることを示します。

赤　001100 xor 001111 = 000011 = 00 00 11
緑　110000 xor 111100 = 001100 = 00 11 00
青　010011 xor 110111 = 100100 = 10 01 00

ビットの立っている位置を見ると、赤は末尾、緑は中央、青は先頭となります。

赤　00 00 11 -> ネスト1の16分割層に納まる（ネスト2層目）
緑　00 11 00 -> 最初の4分割層に納まる（ネスト1層目）
青　10 01 00 -> 分割層なしの層に納まる（ネスト0層目）

となります。

2層目以下の所属階層内では、上位階層の位置は同じになるので、
赤の場合は（001100 001111）
1層目は 00 で、1つ上の層では0位置になります。

0（分割層なし）-1層目（最初の4分割層）については、所属が跨る可能性があり、左上右下両方で1層の番号が同じ場合のみ、1層の位置を示します。

緑　110000 111100 11 = 11　1層目位置は11で3内
青　010011 110111 01! = 11　1層目位置は分割を跨いでいる

【衝突判定】

階層情報でツリーを作成し、衝突判定をおこなってみます。  

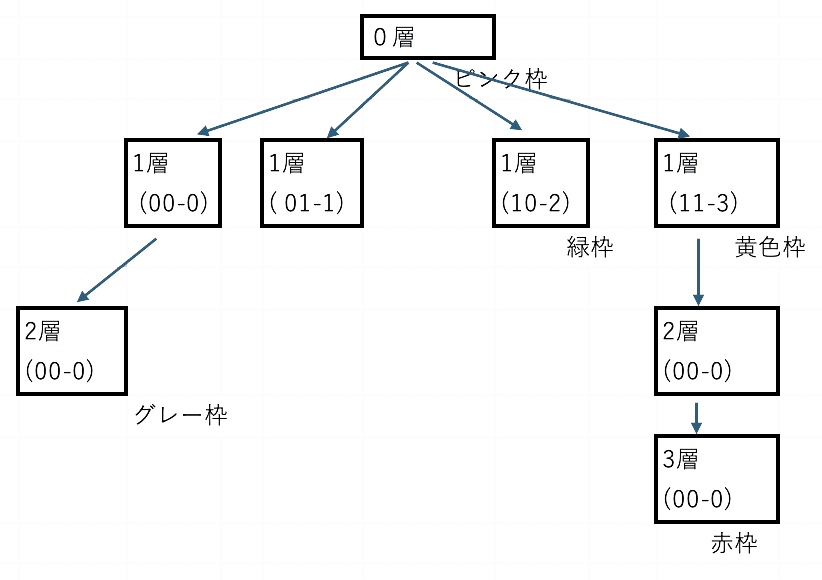
青（2層目）基準にして見てみると

1：先に自分の位置の下のトラバースを取得
　  自分2層下（00 - 0）のものは、必ず自分と衝突する

2：自分の階層
     青色と同じ　1層目インデックスのものはない

3：上1層目のオブジェクト
     黄色については範囲チェック

4：もう一つ上の0層の所属オブジェクト
     ピンク枠は範囲チェック

となります。

【特殊な判定処理例】

一般的な衝突判定の方式について記載していますが、対象や目的によって色々工夫が可能です。

条件1：最下層のサイズが、オブジェクト頂点間サイズとほぼ同じ
条件2：オブジェクトサイズが、全体スケールから見て小さい
条件3：計算速度が最優先

調整1：インデックス全体での一元化により、データの線形アクセスに変更する
調整2：メッシュについて、ボックスでなく頂点別にインデックスをとる

上記のことをおこないます。
　　
インデックス全体での一元化は、以下のイメージです。

連番をK、ネスト数をN、階層がないものの位置をPとすると
K = (4^N-1)/3 + P　
で表せます。

逆も、 
P = K - (4^N-1)/3  
で取れるので、基本を最下層からの処理に限定すれば、親位置にも簡単にアクセス出来ます。

メッシュについてボックスではなく頂点別にインデックスを取るとは、メッシュ内頂点について対角バウンスではなく、それぞれの頂点についてインデックスを計算、連番の配列に登録するということです。

（一部抜粋）

頂点が1分割内に入るように、メッシュサイズと分割の実サイズの調整が必要であることと、メッシュ数により対応頂点数の計算量や保存量が増えますが、全てインデックスの入力だけで衝突や重複順序がわかります。
ここでは記載しませんが、上位層についても同様にインデックスを配置することで、階層間での処理もおこなえます。

【最後に】

モートンオーダーについて検索すると、同じような内容の記事が見つかりますが、ほとんどが2次元でのインデックスの振り方、所属サイズ、取得ビット処理、用途が不明瞭なまま通し番号化の計算（再帰判定なら個人実験ではリンクツリーの方が早い）について書かれているだけで、3次元状態や検索をどのようにするのか、実際の衝突判定をどのようにしているのかは、あまり書かれていませんでした。
条件や優先する内容によっては、同じ階層内や上階層の検索方法についても、他にもいくつか思いつくので、こういった要件なのかもしれません。

またZ曲線以外にも、空間充填をおこなう曲線や、これを使うアルゴリズムが多数存在します。それぞれ特徴があるようなので、ご興味を持たれた方は是非調べて実装してみてください。
最後までご覧いただき、ありがとうございました。

▼G2 Studiosについてはこちら