はじめに

こんにちは！xR・DX事業部で、変なものをあれこれ作っている泉です。

現在、ChatGPTを筆頭にLLMと呼ばれるさまざまな大規模言語モデルが日々公開され、これらのモデル・機能として、大きくTransformer／Attention機構が取り上げられています。

さらにこの土台部分に、言語のベクトル化というものがあり、個人的には一番面白い内容だと思っています。
言語のベクトル化を理解していないと、Attention機構などは全く理解ができないのですが、関連する書籍などでは、「言語トークン」の一言でまとめられてしまっているように感じたので（個人の感想です）、今回はこれらの基幹的な部分である言語のベクトル化について、詳しく解説する記事を書いてみようと思います。

1：言語のベクトル化でできること

まず最初に、簡単に、ベクトル化した言語でどういうことができるのか取り上げます。

ベクトルは「方向」で、座標軸（x1,y1,z1…）で線が描けます。
（※この座標軸をどう作るのかは、後ほど記載します。）
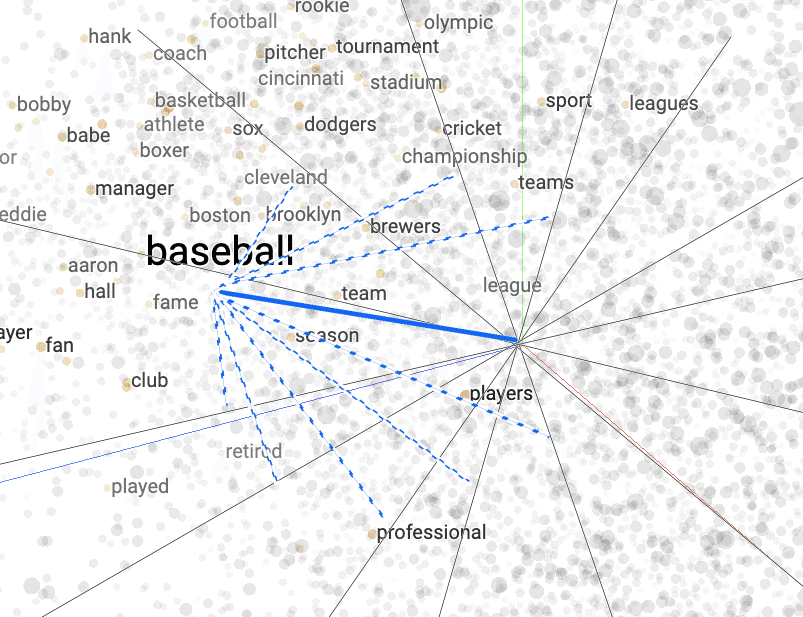
”baseBall”を、多次元のベクトル化をしてみると、下のようなイメージになります。
斜めの座標軸は、本来は直行でお互いに影響しません。

1‐1：演算を通じて、言葉を計算

ベクトル化された言語は、演算を通じて言葉を計算できるようになります。

大規模データ／高次元の学習は手元では無理なので、「text8」という小型の英語学習用データセットを使って、
"football" 足す "racket" 引く "ball"
のように計算し、近いものを列挙してみると（数値は1最大で、類似率のようなもの）

'iihf', 0.68  アイスホッケー連盟
'naia', 0.67  全米大学対抗体育協会
       :
小型のデータセットの短縮での学習結果ですので、結果が微妙ではありますが、一応、足し算引き算でサッカーにラケットを足してボールを取って、アイスホッケーがでてきたので、まぁ合ってる…かな？

1‐2： データ次元の縮小

細かいことは次の節で扱いますが、先ほど小さいと言った「text8」は、一部データをカットした状態で使っていても、3万の単語が存在します。
（分割アルゴリズムは実際には綺麗に分割できないため、単語の切れ端のようなものを多数含みます。)

単純に言語で考えると、英単語だけで数百万存在します。
仮に、1万の単語間の関係を全て記述するとなると、これだけで1億の数値セットが発生します。
先の通り、英単語だけで数百万という状況で、データがとんでもないサイズになり、一単語の関係の計算に、数百万×数百万の演算が発生する可能性があります。

毎回こんな計算をしていたら、ChatGPTに質問を投げて返ってくるまでに何時間かかるのか…電気代もいくらかかるのか…。

ですが、これから見ていくベクトル化によって、ずっと少ないデータで単語の関係を表すことが可能になり、それによってずっと効率的に計算ができるようになります。

2：分散表現や次元の削減など

さて、少し言語から話がそれますが、統計やデータ解析の分野に主成分分析、因子分析というものがあります。マーケティング関連のニュースなどで、このような図を見たことがあるのではないでしょうか。

ニュースでは上の図のような主成分分析を使って商品を分類します。因子分析では少し使い方が異なりますが、「共通要因にこれとこれがある」と判断します。
 
もし今、自分が上のアンケートと同じような表を渡されて、同じようなグラフを作ってほしいと言われたと考えてみると、

質問は、喉越しや後味、香りなどなのに、グラフの縦横の風味、爽快さの軸はどこから来たのだろう？

と思いませんか？

先に言うと、グラフの軸は"なんだかわからない”ものです。
数値は、この”なんだかわからないもの”を基準にした際の各データの位置です。

なんだかよくわからないですよね。
データ分析をする世界でも、これがなんなのかは"結果から"、分析者が"考え"ます。

でもグラフは、縦横2つのXY変数（次元）で、元の関係のないX個のデータ（X次元）をプロットできています。

では、主成分分析の内容をざっと見てみましょう。

まず、数学と理科だけに絞ってみて、図のようにプロットしてみます。
下の図は、縦が数学、横が理科の得点で、各点はその得点を取った生徒を表しています。

右上がりで、なんとなく数学ができれば、理科もできるという感じの全体の流れが見えます。線を引いて、そこに各点を射影してみます。　

これで、数学と理科を合わせた基準ができました。

計算内容の詳細には触れませんが、主成分分析全体では基本的にこれと同じことを、複数の要素の特徴が極力残るように計算します。
　
元データ→データの相互関係を計算し、相関／共分散関係にする

データの特徴を極力残すように、それぞれの分散を最大にする主成分（PC）と呼ぶ軸を作成します。
主成分はいくつも作成できますが、第二主成分まででかなりのデータの特徴を表現できる場合が多いことと、イメージ化する際に都合が良いので、第二まで示しています。

こうして求めた軸を主成分と言い、先のようなグラフでは第一、第二成分を軸としてグラフにしています。

主成分分析でおこなった内容をまとめると、

ということになります。

これは見方を変えると、物事の抽象化であると捉えられます。

例として「綺麗な女性」と言ったとき、それは細かく見ると、目なのか鼻なのか輪郭なのか仕草なのか、それらのバランスのどの部分を指しているのか？となります。
目や鼻や輪郭を上記で入力した部分だと考えれば、綺麗な女性をどうやって判断しているのか、うまく説明はできないけれど、だいたい合意が取れる”感覚上のなにか”が、この軸に当たるということになります。

圧縮される内容は目的によって異なりますが、例えば、画像系の機械学習でも階層的な次元の圧縮をおこなっており、画像の分類や生成をおこなうGANなどのモデルでも、途中にこの過程が存在しています。

3：言語のベクトル化　

なんの話をしていたのか忘れそうですが、主成分分析を例に、ここまで見てきた関係性の抽象化を使うことで、良い感じに基準を作って、良い感じに関係数値を入れていけば、語彙の関係を表現できそうなことはイメージできたかと思います。
ここで、第一ステップは終わりです。

次のステップとして、この軸を決める必要があるのですが、”なんだかわからない軸"のとおり、一体どうやって”なんだかわからない軸"を定義して、数値を振れば良いのでしょうか？

そこで、ここから「Word2Vec」という手法を取り上げますが、この手法は、
「単語の意味は、周囲の単語によって形成される」
という分布仮説に基づいています。

仮説です。

私には、経験則で上手くいってると書いてある以上のことは説明できないので、ここでは基本的な学習動作の流れについて見ていきたいと思います。

「Word2Vec」には、

という2つのアルゴリズムがありますが、今回説明する内容的には違いがないので、統一的に扱います。

先に注意事項をあげ、事前に準備することや、学習時のイメージを見ていきます。

【注意事項】

学習データが文章であること、関連書籍などを見ていると入力文書／単語を、そのままインデックス化しているケースがほとんどなので、入出力を”文章”だと考えがちです。　　
しかし、

この辺りを念頭に置いて、以降をご参照ください。

【事前準備】

1：単語に分解して、インデックスを振る
学習には多数の言葉の入力が必要になります。
下のような文書を多数用意します。

分割アルゴリズム（今回は扱いません）を通して、これを単語に分解・整形します。

それぞれの単語を重複を除いて並べると、

”…”でない部分で、29個あります。

ここで、インデックスを振ります。
ここではとりあえず先のリストの出てきた順でインデックスにします。       
※識別ができればいいので、昇順降順どちらでも問題ありません。

としておきます。 

2：周囲と見なす範囲を決める（Window Size）
入力する語彙についてどこまでを周囲とみなすかの決定をします。

で、”be”を中心に考えると、

となります。
サイズが小さいと学習は早いですが、複雑な文書に対しての応用が無くなり、広くとり過ぎると、あまり関係のない内容でも関連ができてしまい、出力内容が不安定になります。
この辺りも、必要とコストに応じて決定される内容で、明確な数値はありません。 

3：OneHotベクトルと教師データを作成
上記の注1で記した通り、入力は単語を識別するインデックスの指定です。

先に、IDを

としました。
   
今回、29個の他、合わせて100個の単語があるとして、
学習する対象を、

の”be”だとします。

”be”のIDは16なので、OneHotベクトルは16番目に1が立ち

になります。

先の周辺1の“will”,“lost” は

です。

入力した”be”に対するWindowSize=1の学習における教師データ（正解）として、

を準備します。

4：圧縮する次元を決める
入力の単語数に対し、いくつの”なんだかわからない”軸を作るか決めます。
これは、入力する規模に応じて決定されます。
※次の学習過程の図では、ここでお話しした圧縮する次元を10にしています。

【学習過程】

Skip-Gramのアルゴリズムで、言語ベクトルを作るネットワークは以下のようになります。
GBowの場合は前後逆になりますが、意味合いは同じですので、こちらで解説します。 

学習するシステムなので、重さ行列の記載のある大きな2つのボックスは、最初はランダムな数値が入ります。

準備で作成したOneHotベクトル1つにつき、以下の作業を繰り返していきます。

1：入力にOneHotベクトル1つセット
100個のうち、1つだけ1が立っているベクトル
例：先ほどの “be”だと
 (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0 ….. ) 

2：1つ目の重さ行列を掛けて、次元の少ない隠れ層を計算
例：10個になる
(0.94,0.22,0.32,0.85,0.12,0.21,0.33,0.54,0.11,0.13)

3：2つ目の重さ行列を掛けて次元を戻す
例：100個の数値列
(0.00, 0.00 ,0.00 ,0.00 ,0.00 ,2.00 ,1.55, 4.42 ,2.81 ,0,0 ….. ) 

4：0..1の確率化　
softMaxには触れませんが、各項目の数値が0..1の比率になるようにし、出現確率として扱えるようにします。
 (0.00, 0.00 ,0.00 ,0.00 ,0.00 ,1.00 ,0.84, 0.22 , 0.42 ,0,0 ….. ) 

5：結果の比較からの補正
先の “be” では、
input: (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0 ….. ) 

あるべき結果は、
(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0 ….. )  
(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0 ….. )  
        
でしたので、上記の4の
(0.00, 0.00 ,0.00 ,0.00 ,0.00 ,2.00 ,1.55, 4.42 ,2.81 ,0,0 ….. ) 
と比較。
計算については説明しませんが、差分をとって逆向きに偏微分する形で、上記2と3の重さ行列を修正する。
　　　
6：正解が出るまで繰り返す

7：次のOneHotベクトルを入力

となります。

最後に、重さ行列の修正についてですが、
入力を（x1,x2,x3,,,,,,,）、重さ行列を（Wij ij=行列位置）、 隠れ層を（y1,y2,y3…）とすると、y1 = x1 * W11 +  x1 * W12 + ……となり、これは内積になっています。

内積は、一方を基底と見た射影計算のようなもので、ベクトル間の類似度／角度を示す指標として使用されます。
 
要するに、一番最初の軸がたくさんある”BaseBall”のイメージのように、各単語のベクトルの隠し層の基準に対する角度（多次元ですが…）を調整している、という訳です。

最後に…

めんどくさい計算の部分を端折りまくっていますが、言語ベクトル化を通じて、機械学習に関する次元圧縮や、これらの行列演算の一旦についてイメージできたでしょうか？
LLMだと、ここからまだAttention機構という最重要項目が残っています。

端的に言うとAttention機構は、ベクトル化した単語を最初の例のように演算して、より目的にあった位置に移動する、という内容です。
またそのうち、こちらについてもまとめてみようと思っていますので、お楽しみに！

▼G2 Studiosについてはこちら